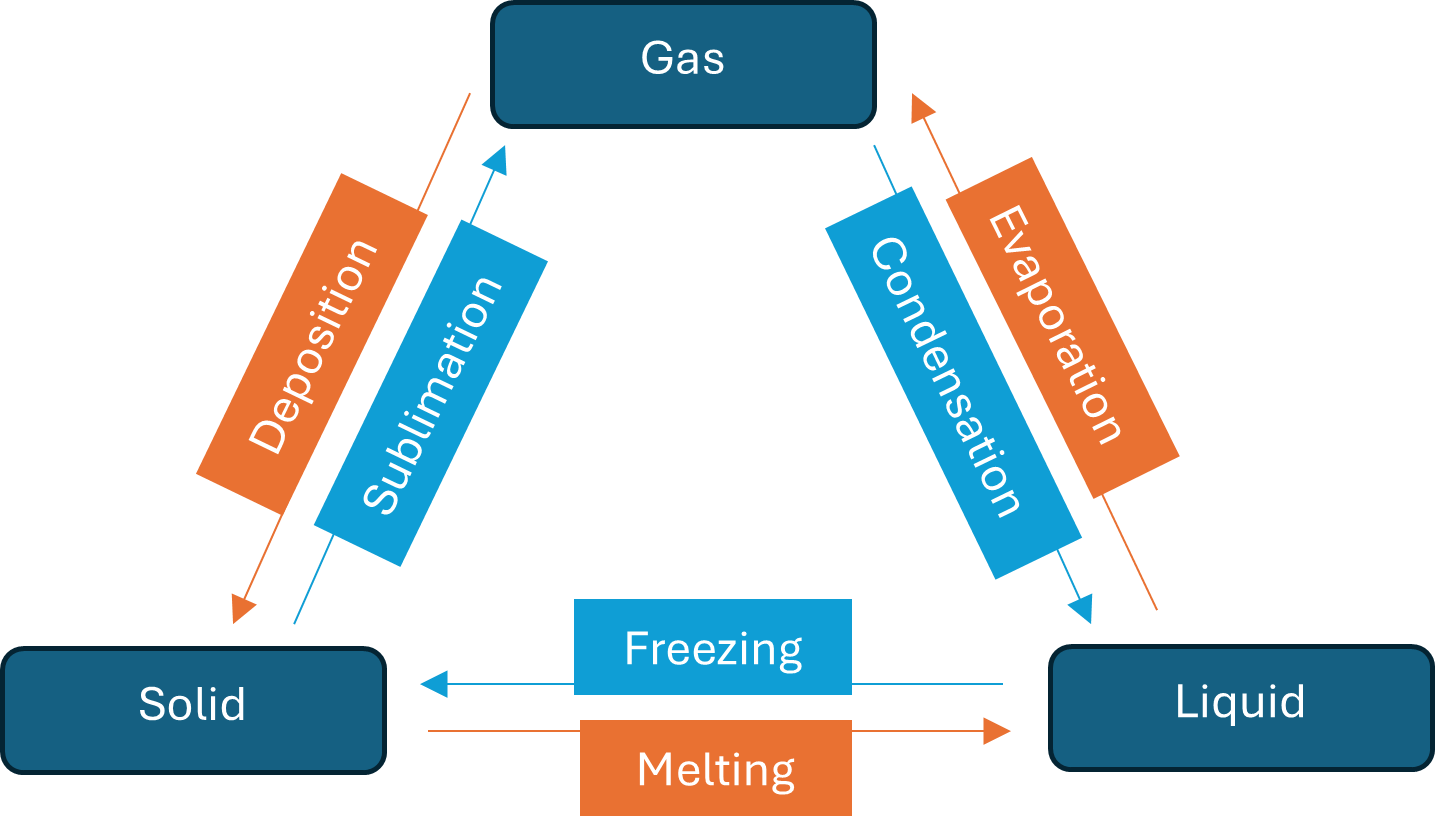
Topic 2.2.2: Internal Energy and Specific Heat Capacity
Rise in Temperature and Increase in Internal Energy
When the temperature of an object increases, its internal energy also increases. This is because the increase in temperature results in an increase in the average kinetic energy of the particles within the object. The internal energy of an object is the total energy of all its particles, including both the kinetic energy due to their motion and the potential energy due to the forces between them.
Increase in Temperature and Kinetic Energy of Particles
The temperature of an object is directly related to the average kinetic energy of its particles. When an object is heated, the particles within the object begin to move more rapidly. This increase in the motion of the particles corresponds to an increase in their kinetic energy, which in turn increases the overall internal energy of the object.
Specific Heat Capacity
Specific heat capacity is defined as the amount of energy required to raise the temperature of one kilogram of a substance by one degree Celsius (or one Kelvin). The equation for specific heat capacity is:
Equation:
\[
c = \frac{\Delta E}{m \Delta \theta}
\]
Where:
- c is the specific heat capacity (J/kg°C or J/kg·K)
- ΔE is the energy added (J)
- m is the mass of the substance (kg)
- Δθ is the change in temperature (°C or K)
This equation allows us to calculate how much energy is required to heat a substance, depending on its mass, the temperature change, and its specific heat capacity.
Experiments to Measure Specific Heat Capacity of Solids and Liquids
Experiment to Measure Specific Heat Capacity of a Solid:
To measure the specific heat capacity of a solid, one common method is to use an electrical heater and a calorimeter. The solid is placed in thermal contact with the heater, and the temperature change is recorded over time. The amount of electrical energy supplied by the heater is calculated, and using the equation for specific heat capacity, the specific heat capacity of the solid can be determined.
Experiment to Measure Specific Heat Capacity of a Liquid:
For liquids, a similar approach is used. A known amount of liquid is placed in a calorimeter, and an electrical heater is used to heat the liquid. The temperature change of the liquid is measured, and the energy supplied by the heater is calculated. By applying the specific heat capacity equation, the specific heat capacity of the liquid can be determined.
Practice Problems: Internal Energy and Specific Heat Capacity
Problem 1: Calculating Energy Required to Heat a Solid
Question: A 0.5 kg piece of metal is heated from 20°C to 80°C. If the specific heat capacity of the metal is \( 900 \, \text{J/kg°C} \), calculate the amount of energy required to heat the metal.
Solution:
Using the formula for specific heat capacity:
\[
\Delta E = m c \Delta \theta
\]
Substitute the known values:
\[
\Delta E = 0.5 \times 900 \times (80 - 20) = 0.5 \times 900 \times 60 = 27,000 \, \text{J}
\]
Answer: The energy required is 27,000 J.
Problem 2: Specific Heat Capacity of a Liquid
Question: A 1.2 kg sample of water is heated from 15°C to 50°C, and the energy supplied is 42,000 J. Calculate the specific heat capacity of the water.
Solution:
Using the formula for specific heat capacity:
\[
c = \frac{\Delta E}{m \Delta \theta}
\]
Substitute the known values:
\[
c = \frac{42,000}{1.2 \times (50 - 15)} = \frac{42,000}{1.2 \times 35} = \frac{42,000}{42} = 1000 \, \text{J/kg°C}
\]
Answer: The specific heat capacity of the water is 1000 J/kg°C.
Problem 3: Temperature Change and Energy
Question: If 5,000 J of energy is supplied to a 2.0 kg block of copper, causing its temperature to rise from 20°C to 40°C, calculate the specific heat capacity of copper.
Solution:
Using the formula for specific heat capacity:
\[
c = \frac{\Delta E}{m \Delta \theta}
\]
Substitute the known values:
\[
c = \frac{5,000}{2.0 \times (40 - 20)} = \frac{5,000}{2.0 \times 20} = \frac{5,000}{40} = 125 \, \text{J/kg°C}
\]
Answer: The specific heat capacity of copper is 125 J/kg°C.
Problem 4: Energy Required to Heat a Liquid
Question: A 3.0 kg sample of oil is heated from 25°C to 75°C. If the specific heat capacity of the oil is 1,800 J/kg°C, calculate the total energy required to heat the oil.
Solution:
Using the formula for specific heat capacity:
\[
\Delta E = m c \Delta \theta
\]
Substitute the known values:
\[
\Delta E = 3.0 \times 1,800 \times (75 - 25) = 3.0 \times 1,800 \times 50 = 270,000 \, \text{J}
\]
Answer: The energy required is 270,000 J.
Problem 5: Increase in Internal Energy
Question: A 0.25 kg piece of aluminum is heated and its temperature increases from 30°C to 80°C. If the specific heat capacity of aluminum is 900 J/kg°C, calculate the increase in internal energy.
Solution:
Using the formula for specific heat capacity:
\[
\Delta E = m c \Delta \theta
\]
Substitute the known values:
\[
\Delta E = 0.25 \times 900 \times (80 - 30) = 0.25 \times 900 \times 50 = 11,250 \, \text{J}
\]
Answer: The increase in internal energy is 11,250 J.